Поиск
| Автор | Сообщение |
|---|---|
|
trick
#
18 июн 2012 |
|
|
o_a
#
18 июн 2012 |
|
|
trick
#
19 июн 2012 |
|
|
o_a
#
19 июн 2012 |
|
|
trick
#
19 июн 2012 trick
19 июн 2012
|
|
|
o_a
#
19 июн 2012 |
|
|
trick
#
19 июн 2012 |
|
|
trick
#
19 июн 2012 |
|
|
o_a
#
20 июн 2012 |
|
|
trick
#
24 июн 2012 trick
24 июн 2012
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
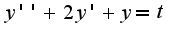 при
при 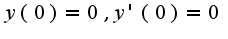 по теореме дифференцирования
по теореме дифференцирования 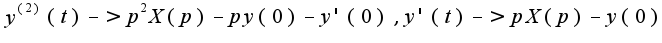 Учитывая начальные условия, получим уравнение
Учитывая начальные условия, получим уравнение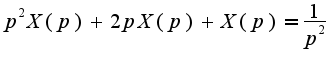 Сл-но,
Сл-но,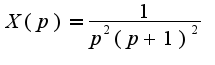 Разлагая это выражение на сумму дробей, получим
Разлагая это выражение на сумму дробей, получим 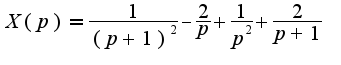 Чем воспользовались для разложение на простые дроби, как это получилось?
А также это уравнение нужно решить, так сказать, линейным способом.
Я не могу разобраться... оно решается через характеристическое уравнение? Если так, то у меня ответ не совпадает с вашим, полученным при решении операционным методам...
То есть ответ в обоих способах вероятно должен быть таким
Чем воспользовались для разложение на простые дроби, как это получилось?
А также это уравнение нужно решить, так сказать, линейным способом.
Я не могу разобраться... оно решается через характеристическое уравнение? Если так, то у меня ответ не совпадает с вашим, полученным при решении операционным методам...
То есть ответ в обоих способах вероятно должен быть таким 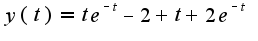 2)
По рядам
По графику нужно разложить в ряд Фурье, тут яб хотел чтобы помогли, проверить решение.
Для кусочно-гладкой на отрезке
2)
По рядам
По графику нужно разложить в ряд Фурье, тут яб хотел чтобы помогли, проверить решение.
Для кусочно-гладкой на отрезке ![$[-l,l]$ $[-l,l]$](http://teacode.com/service/latex/latex.png?latex=%5B-l%2Cl%5D&fontsize=21) функции :
функции : 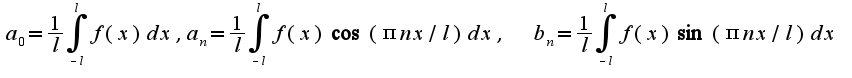 .
a)
Очевидно что для данного графика l=2
b)
.
a)
Очевидно что для данного графика l=2
b)
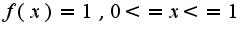
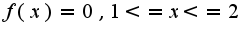 c)
c)
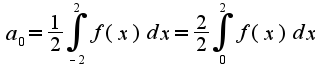 подставляем начальные условия
подставляем начальные условия
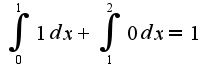 d)
d)
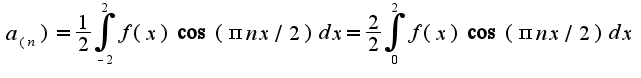 также подставляем начальные условия
также подставляем начальные условия
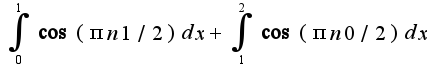 далее у меня получилась ерунда, которая скорее всего связана с тем что, у меня проблемы с интегрированием.
далее у меня получилась ерунда, которая скорее всего связана с тем что, у меня проблемы с интегрированием.
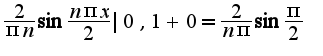 Выглядит это уж слишком неверно, как мне кажется, вычислять
Выглядит это уж слишком неверно, как мне кажется, вычислять 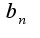 не брался потому, как там схожая проблема с интегралом только с косинусом =\
не брался потому, как там схожая проблема с интегралом только с косинусом =\
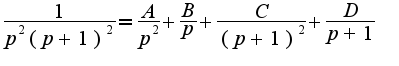 b)решение можно найти в учебнике по д.у.сначала ищется решение соответствующего однородного уравнения, затем неоднородного, сумма этих решений дает результат
подобные примеры решены в темах данной консультации
2) неверно найден период, он равен
b)решение можно найти в учебнике по д.у.сначала ищется решение соответствующего однородного уравнения, затем неоднородного, сумма этих решений дает результат
подобные примеры решены в темах данной консультации
2) неверно найден период, он равен 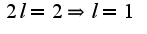 , поэтому неверно найдены коэффициенты ряда
, поэтому неверно найдены коэффициенты ряда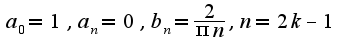
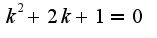
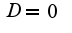
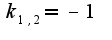 общее решение имеет вид
общее решение имеет вид
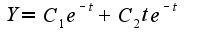 подставим начальные условия
подставим начальные условия
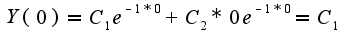
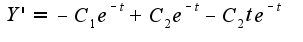
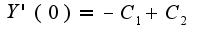 составим систему
составим систему
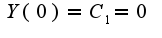
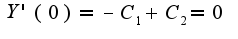 '
ну и отсюда следует что С1 и C2 = 0
подставляем в общее решение
'
ну и отсюда следует что С1 и C2 = 0
подставляем в общее решение
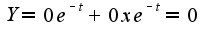 где я ошибаюсь? =\
где я ошибаюсь? =\
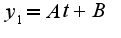 . Нужно подставить в данное уравнение и найти
. Нужно подставить в данное уравнение и найти 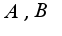
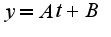
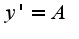
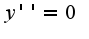
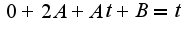 ищем abc
ищем abc
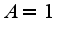
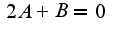
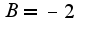 подставляем в исходное
подставляем в исходное
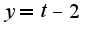 вроде поправил крайне глупую ошибку..
верно?
вроде поправил крайне глупую ошибку..
верно?
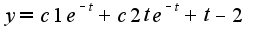 Подставьте в него начальные условия, чтобы найти
Подставьте в него начальные условия, чтобы найти 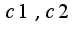
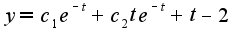
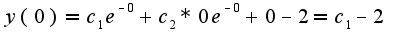
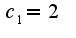
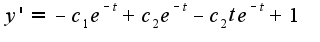
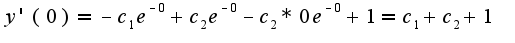
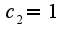 если я опять ничего не напутал выходит...
если я опять ничего не напутал выходит...
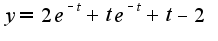 Сошлось с операционным вычислением) значит верно))
Огромное спасибо. Как я могу вас поблагодарить?)
Сошлось с операционным вычислением) значит верно))
Огромное спасибо. Как я могу вас поблагодарить?)
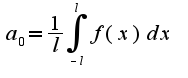
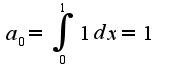 далее
далее
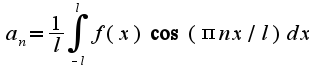
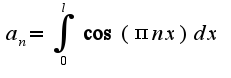
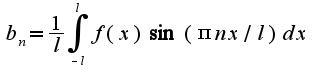
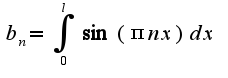 это верно?
это верно?
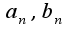 )в пределах от нуля до единицы
)в пределах от нуля до единицы