Поиск
| Автор | Сообщение |
|---|---|
|
Наталия
#
19 окт 2006 |
|
|
О.А.
#
19 окт 2006 |
|
|
О.А.
#
19 окт 2006 |
|
|
Наталия
#
20 окт 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
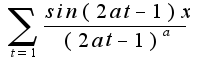 Решение:
Используем признак сходимости Абеля
Положим, что х – фиксированная величина, причем
Введем замену:
Решение:
Используем признак сходимости Абеля
Положим, что х – фиксированная величина, причем
Введем замену:
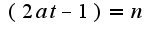 Тогда ,
Тогда ,
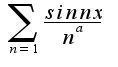
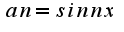
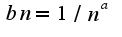 Проверим два условия:
1. Один из сомножителей имеет ограниченную первообразную,
2. Второй монотонно убывающий и предел при n стрем к бескон. равен нулю.
Проверим два условия:
1. Один из сомножителей имеет ограниченную первообразную,
2. Второй монотонно убывающий и предел при n стрем к бескон. равен нулю.
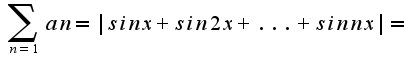
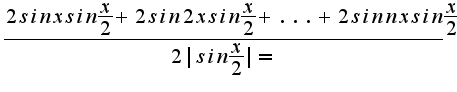
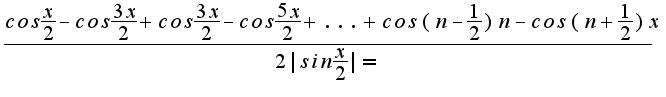
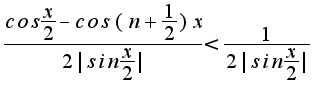
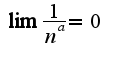 следовательно ряд сходится.
Так?
как теперь найти область сходимости ряда? исходя из уже полученного? т.е.:
следовательно ряд сходится.
Так?
как теперь найти область сходимости ряда? исходя из уже полученного? т.е.:
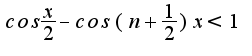 ?
заранее спасибо
?
заранее спасибо
 , при которых сходится данный Функциональный ряд, а не числовой. Можно исследовать на равномерную сходимость, используя признак равномерной сходимости Абеля-Дирихле. Формулировка его та же, но в терминах равномерной сходимости. Вы правильно провели оценку для частичных сумм ряда, только надо исключить равенство знаменателя нулю, т.е.
, при которых сходится данный Функциональный ряд, а не числовой. Можно исследовать на равномерную сходимость, используя признак равномерной сходимости Абеля-Дирихле. Формулировка его та же, но в терминах равномерной сходимости. Вы правильно провели оценку для частичных сумм ряда, только надо исключить равенство знаменателя нулю, т.е.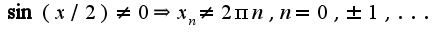 Таким образом, ряд сходится равномерно на любом фиксированном сегменте, не содержащем точек
Таким образом, ряд сходится равномерно на любом фиксированном сегменте, не содержащем точек