Поиск
| Автор | Сообщение |
|---|---|
|
Настена
#
16 июн 2008 |
|
|
О.А.
#
16 июн 2008 |
|
|
Настена
#
17 июн 2008 |
|
|
О.А.
#
17 июн 2008 |
|
|
Настена
#
17 июн 2008 |
|
|
Настена
#
18 июн 2008 |
|
|
Настена
#
19 июн 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
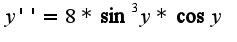
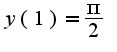
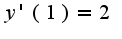
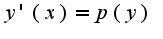
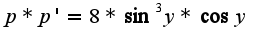
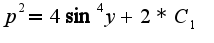
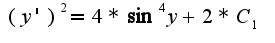
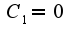
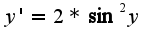
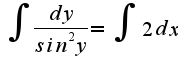
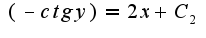
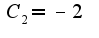
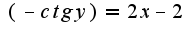
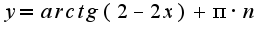
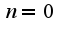
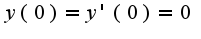
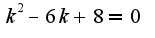
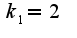
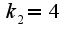 общее решение однородного уравнения
y=C1*e^2^x+C2*e^(4x)
C'1(x)e^2^x+C2'(x)e^4^x=0
2C'1(x)e^2^x+4C'2(x)e^4^x={e4^2x}:{1+e^-2x}
C'1(x)=-C'2(x)e^2x
-2C'2(x) e^2x e^2x+4C'2(x)e^4x={e4^2x}:{1+e^-2x}
C'2(x)={2e^-^2^x}:{1+e^-2x}
C'1={-2}:{1+e^-^2x}
C1(x)={-2dx}:{1+e^-2x}
C2(x)={2e^(-2x) dx}:{1+e^-2x}
туплю, конечно, но как высчитать эти интегралы?
да и вообще опять таки проверьте, пожалуйста, все решение на ошибки... без них что-то не обходится...
общее решение однородного уравнения
y=C1*e^2^x+C2*e^(4x)
C'1(x)e^2^x+C2'(x)e^4^x=0
2C'1(x)e^2^x+4C'2(x)e^4^x={e4^2x}:{1+e^-2x}
C'1(x)=-C'2(x)e^2x
-2C'2(x) e^2x e^2x+4C'2(x)e^4x={e4^2x}:{1+e^-2x}
C'2(x)={2e^-^2^x}:{1+e^-2x}
C'1={-2}:{1+e^-^2x}
C1(x)={-2dx}:{1+e^-2x}
C2(x)={2e^(-2x) dx}:{1+e^-2x}
туплю, конечно, но как высчитать эти интегралы?
да и вообще опять таки проверьте, пожалуйста, все решение на ошибки... без них что-то не обходится...
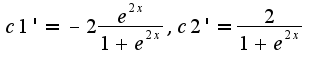 первый интеграл табличный, второй приводится ктабличному заменой
первый интеграл табличный, второй приводится ктабличному заменой 