Поиск
| Автор | Сообщение |
|---|---|
|
susan
#
28 ноя 2013 |
|
|
o_a
#
28 ноя 2013 |
|
|
alina
#
28 ноя 2013 |
|
|
o_a
#
29 ноя 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
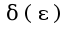 А именно,
А именно, ![$\forall \epsilon>0\exists \delta(\epsilon)>0\forall x1,x2\in[-2,5]:|x1-x2|<\delta\Rightarrow |x1^2-2x1-1-x2^2+2x2+1|=$ $\forall \epsilon>0\exists \delta(\epsilon)>0\forall x1,x2\in[-2,5]:|x1-x2|<\delta\Rightarrow |x1^2-2x1-1-x2^2+2x2+1|=$](http://teacode.com/service/latex/latex.png?latex=%5Cforall+%5Cepsilon%3E0%5Cexists+%5Cdelta%28%5Cepsilon%29%3E0%5Cforall+x1%2Cx2%5Cin%5B-2%2C5%5D%3A%7Cx1-x2%7C%3C%5Cdelta%5CRightarrow+%7Cx1%5E2-2x1-1-x2%5E2%2B2x2%2B1%7C%3D&fontsize=21)
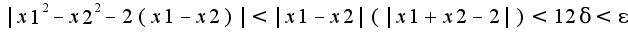 Из последнего неравенства следует, что
Из последнего неравенства следует, что 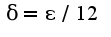
![$x1,x2\in[-2,5]\Rightarrow x1<5,x2<5\Rightarrow |x1+x2-2|\leq |x1|+|x2|+2\leq 12$ $x1,x2\in[-2,5]\Rightarrow x1<5,x2<5\Rightarrow |x1+x2-2|\leq |x1|+|x2|+2\leq 12$](http://teacode.com/service/latex/latex.png?latex=x1%2Cx2%5Cin%5B-2%2C5%5D%5CRightarrow+x1%3C5%2Cx2%3C5%5CRightarrow+%7Cx1%2Bx2-2%7C%5Cleq+%7Cx1%7C%2B%7Cx2%7C%2B2%5Cleq+12&fontsize=21)