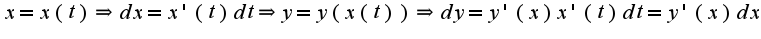Sonechka
#
5 янв 2011
|
Здравствуйте, Ольга Александровна, с наступившим Вас!
у меня к вам вопрос по экзаменационным билетам. Когда мы разбирали функцию Дирихле,то пришли к выводу, что она не является непрерывной. Можете подсказать ход рассуждений,т.е. как мы нашли дельта D и как, применив аксиому полноты, пришли к выводу,что она разрывна?
Заранее спасибо.
|
o_a
#
6 янв 2011
|
Здравствуйте, Соня. Спасибо, и Вас тоже с Новым годом! Пусть точка 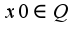 тогда 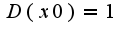 Тогда в силу аксиомы полноты в любой окрестности данной точки существуют иррациональные точки, в них 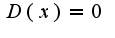 Поэтому, 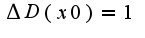 Аналогичные рассуждения и для выбора точки 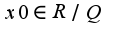 Таким образом,функция Дирихле разрывна во всех точках,т.к. на любом интервале есть как рациональные, так и иррациональные точки в силу аксиомы полноты, для данной функции приращение принимает значение 1
|
katyatkach2141
#
6 янв 2011
|
Ольга Александровна, возник такой вопрос. В теореме Вейерштрасса о непрерывной функции не получается провести доказательство для функции, ограниченно
|
katyatkach2141
#
6 янв 2011
|
Ольга Александровна, возник такой вопрос. В теореме Вейерштрасса о непрерывной функции не получается провести доказательство для функции, ограниченной снизу. Подскажите, пожалуйста, ход рассуждений.
Заранее благодарна.
|
o_a
#
6 янв 2011
|
Нужно доказывать от противного. Возьмем последовательность неограниченную снизу 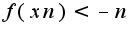 Так как функция непрерывна на отрезке, то любая подпоследовательность 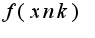 должна сходится к 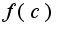 при условии, что 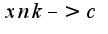 причем, ![$xnk\in[a,b],c\in[a,b]$ $xnk\in[a,b],c\in[a,b]$](http://teacode.com/service/latex/latex.png?latex=xnk%5Cin%5Ba%2Cb%5D%2Cc%5Cin%5Ba%2Cb%5D&fontsize=21) Однако, если последовательность бесконечно большая, то и любая подпоследовательность должна быть бесконечно большой, что противоречит вышенаписанному условию сходимости
|
Sonechka
#
7 янв 2011
|
Спасибо большое,но у меня появился еще вопрос.
Ольга Александровна,можете подсказать,как доказывать,что lim(x_n*y_n)=A*B при n->infinity? (из билета про арифметические операции над последовательностями)
|
o_a
#
7 янв 2011
|
Известна лемма 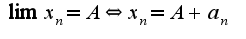 Сл-но, 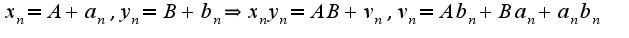 Поэтому, 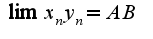
|
Sonechka
#
7 янв 2011
|
спасибо.
|
katyatkach2141
#
8 янв 2011
|
Ольга Александровна, как определить, какое условие существования локального экстремума нужно применять для нахождения производной? И как понять,подходит ли нам данное условие или нет?
|
o_a
#
8 янв 2011
|
Катя, о чем идет речь, трудно понять из Вашего вопроса. Есть три достаточных условия для нахождения локального экстремума. Если функция дифференцируема в окрестности точки, то, как правило, применяют первое достаточное условие, ну, и иногда, если трудно исследовать изменение знака при переходе через стационарную точку, то применяют второе достаточное условие, и совсем редко встречающиеся функции, для которых не действуют вышеуказанные два, то третье достаточное условие. Этот материал подробно изложен в учебнике под редакцией В.А. Садовничего. Если же функция не диф. в самой стационарной точке, но непрерывна в ней, то используют аналог первого достаточного условия, например, для функции 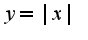 , производная которой меняет знак при переходе через 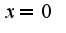 , которая является точкой минимума данной функции. В нуле функция непрерывна, но не диф.
|
MaxOshirov2141
#
9 янв 2011
|
Ольга Александровна, с прошедшими вас праздниками! У меня назрел вопрос по инвариантности формы первого дифференциала. Какова суть данного утверждения? Выражаясь тривиально, этот дифференциал постоянен и не имеет иных форм, я верно понимаю? Но затруднение вызывает доказательство данного утверждения. В википедии доказательство мне непонятно, а в лекции я успел записать только выкладки безо всяких комментариев. Не поможете разобраться?
|
o_a
#
9 янв 2011
|
Здравствуйте, Максим! Спасибо, Вас также с праздниками!
Вид первого дифференциала, а именно 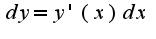 сохраняется независимо от того, является ли 1)  -независимая переменная,2) 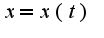 -является функцией от 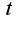 Доказательство второго утверждение проводится с использованием теоремы о дифференцировании сложной функции, действительно, если 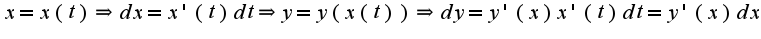
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
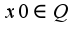 тогда
тогда 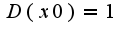 Тогда в силу аксиомы полноты в любой окрестности данной точки существуют иррациональные точки, в них
Тогда в силу аксиомы полноты в любой окрестности данной точки существуют иррациональные точки, в них 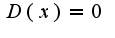 Поэтому,
Поэтому, 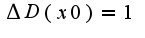 Аналогичные рассуждения и для выбора точки
Аналогичные рассуждения и для выбора точки 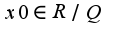 Таким образом,функция Дирихле разрывна во всех точках,т.к. на любом интервале есть как рациональные, так и иррациональные точки в силу аксиомы полноты, для данной функции приращение принимает значение 1
Таким образом,функция Дирихле разрывна во всех точках,т.к. на любом интервале есть как рациональные, так и иррациональные точки в силу аксиомы полноты, для данной функции приращение принимает значение 1
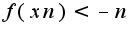 Так как функция непрерывна на отрезке, то любая подпоследовательность
Так как функция непрерывна на отрезке, то любая подпоследовательность 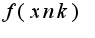 должна сходится к
должна сходится к 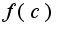 при условии, что
при условии, что 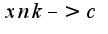 причем,
причем, ![$xnk\in[a,b],c\in[a,b]$ $xnk\in[a,b],c\in[a,b]$](http://teacode.com/service/latex/latex.png?latex=xnk%5Cin%5Ba%2Cb%5D%2Cc%5Cin%5Ba%2Cb%5D&fontsize=21) Однако, если последовательность бесконечно большая, то и любая подпоследовательность должна быть бесконечно большой, что противоречит вышенаписанному условию сходимости
Однако, если последовательность бесконечно большая, то и любая подпоследовательность должна быть бесконечно большой, что противоречит вышенаписанному условию сходимости
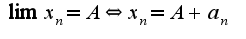 Сл-но,
Сл-но, 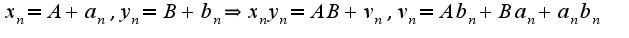 Поэтому,
Поэтому,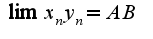
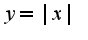 , производная которой меняет знак при переходе через
, производная которой меняет знак при переходе через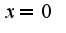 , которая является точкой минимума данной функции. В нуле функция непрерывна, но не диф.
, которая является точкой минимума данной функции. В нуле функция непрерывна, но не диф.
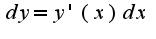 сохраняется независимо от того, является ли 1)
сохраняется независимо от того, является ли 1) -независимая переменная,2)
-независимая переменная,2)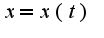 -является функцией от
-является функцией от 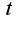 Доказательство второго утверждение проводится с использованием теоремы о дифференцировании сложной функции, действительно, если
Доказательство второго утверждение проводится с использованием теоремы о дифференцировании сложной функции, действительно, если