Поиск
| Автор | Сообщение |
|---|---|
|
Darksider
#
29 окт 2014 |
|
|
o_a
#
29 окт 2014 |
|
|
Darksider
#
29 окт 2014 |
|
|
o_a
#
29 окт 2014 |
|
|
Darksider
#
29 окт 2014 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
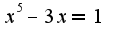 Доказать, что уравнение имеет хотя бы один корень на отрезке [1,2]
2.
Доказать, что уравнение имеет хотя бы один корень на отрезке [1,2]
2.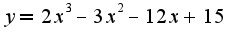 обращается ли в нуль функция где-нибудь на отрезке [1,3]
обращается ли в нуль функция где-нибудь на отрезке [1,3]
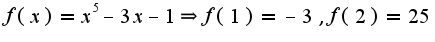 , поэтому есть хотя бы один корень уравнения.
, поэтому есть хотя бы один корень уравнения.