Страницы: 1 2 3 4 5 6 7 8 9 10 11
Поиск| Автор | Сообщение |
|---|---|
|
О.А.
#
21 сен 2009 |
|
|
Михаил
#
21 сен 2009 |
|
|
Михаил
#
21 сен 2009 |
|
|
О.А.
#
21 сен 2009 |
|
|
Михаил
#
21 сен 2009 |
|
|
О.А.
#
21 сен 2009 |
|
|
Михаил
#
23 сен 2009 |
|
|
Лиля
#
4 окт 2009 |
|
|
О.А.
#
4 окт 2009 |
|
|
Саша
#
4 окт 2009 |
|
|
Саша
#
4 окт 2009 |
|
|
Лиля
#
5 окт 2009 |
|
|
И.К.
#
16 окт 2009 |
|
|
О.А.
#
16 окт 2009 |
|
|
И.К.
#
16 окт 2009 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11
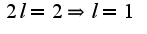 поэтому коэффициенты общего ряда Фурье находятся по формулам
поэтому коэффициенты общего ряда Фурье находятся по формулам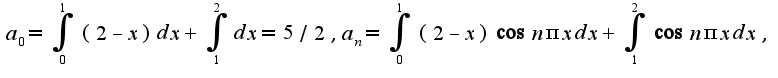
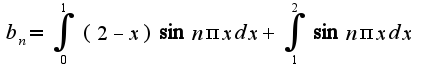
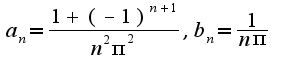
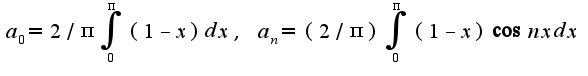
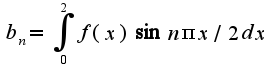 что касается ответа, можно попробовать упростить, используя свойства синуса и косинуса, а можно оставить в первоначальном виде
что касается ответа, можно попробовать упростить, используя свойства синуса и косинуса, а можно оставить в первоначальном виде
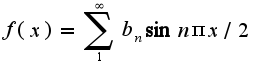
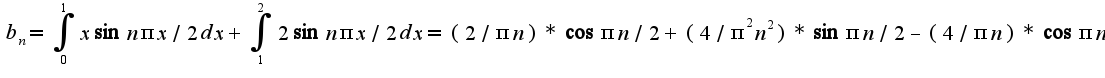 Как можно упростить это выражение?
Знаю, что
Как можно упростить это выражение?
Знаю, что 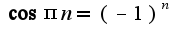 . А что можно сделать с
. А что можно сделать с 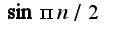 ?
Подскажите пожалуйста!
?
Подскажите пожалуйста!