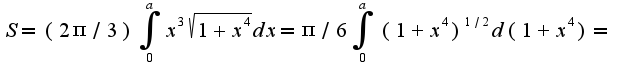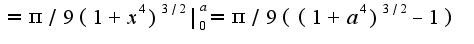Поиск
| Автор | Сообщение |
|---|---|
|
distvamp
#
27 ноя 2016 |
|
|
o_a
#
27 ноя 2016 |
|
|
distvamp
#
27 ноя 2016 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
 Для данного примера она получается в виде
Для данного примера она получается в виде